FÍSICA I

FÍSICA

La palabra física procede del vocablo griego que significa naturaleza, pudiéndose decir que la Física es una rama de la Filosofía Natural y estudia las propiedades básicas del Universo y por tanto está regida por los inalterables principios que la naturaleza impone.

La Física, como todas las Ciencias Experimentales, es el producto de un largo proceso de investigación efectuado con dedicación, paciencia y esfuerzo.

Los principios, leyes y teorías que conforman la Física son el resultado del trabajo metódico y constante de muchos investigadores preocupados por interpretar los hechos y los fenómenos que ocurren en el universo.

Los científicos, para lograr sus objetivos, no proceden desordenadamente ni respondiendo a súbitas inspiraciones, sino que lo hacen siguiendo planes adecuadamente preparados.

Los investigadores, cuando se enfrentan a un problema cuya solución les es desconocida, se sienten estimulados por la curiosidad y adoptan una actitud fuertemente inquisitiva. En sus mentes surgen diversos interrogantes que tratan de responder efectuando una serie organizada de acciones y procesos.

Estos procesos constituyen lo que se llama método experimental o científico

El método científico o experimental

La Física trata de dar contestación a los fenómenos de la Naturaleza, fenómenos de cada día, de cada instante, comienza por dar al hombre que la trabaja un agudo espíritu de observación, obligándole en todo momento a preguntarse los motivos (¿por qué?) de ciertos cambios que su medio material experimenta. Al no contentarse con un mero «por que sí» se obliga a recorrer todos los conocimientos que de éstas y otras disciplinas tiene, aunque es probable que previo a este análisis memorístico, trate de clasificar el fenómeno. Su imaginación juega, sus sentidos observan y analizan, su inteligencia determina, llegando en un alto porcentaje de los casos a la conclusión de que la Física puede darle una respuesta aclaratoria del fenómeno observado.

Esta inquietud del hombre condicionada a su razón, tratando de explicarse los fenómenos que ocurren a su alrededor, hace que se organice sistemáticamente, estableciéndose un método para encontrar respuestas a sus interrogantes: observación, razonamiento y experimentación constituyen lo que llamamos el Método Científico; no necesariamente este proceso sigue el orden que hemos establecido, piénsese, por ejemplo, en los trabajos de Dimitri I. Mendeléiev (1834-1907) ordenando los elementos en lo que hoy se denomina sistema periódico, atreviéndose a dejar huecos prediciendo la existencia de elementos desconocidos hasta entonces, adelantándose la razón a la observación. Muy frecuentemente, trabajos realizados por los que han sido llamados físicos teóricos y que a primera vista parecen puramente teóricos y abstractos, encuentran con el tiempo las más diversas aplicaciones técnicas.

En el estudio de la Física en general, las Matemáticas constituyen la herramienta fundamental en la descripción del comportamiento físico; sin embargo, la descripción perfectamente pormenorizada no es posible debido al comportamiento anárquico de la naturaleza en muchas de sus facetas. La aplicación de las Matemáticas a un fenómeno físico implica un conocimiento exhaustivo del problema, su formulación matemática representa un modelo o descripción límite ideal, que se aproxima, pero nunca alcanza por completo la situación física real.

El estudiante debe tener un proceso dual en su mente, debe pensar en la situación física y también de acuerdo con la descripción matemática correspondiente; al construir el modelo matemático idealizado, para su aplicación a un problema real, debe conocer las limitaciones y aproximaciones que se han realizado y por supuesto tener conocimiento de las consecuencias que pueden tener, en muchos casos decimos que no influyen o que son despreciables. Esta aproximación es totalmente válida en un conocimiento en que es aplicada al problema técnico, siempre que los efectos de esta aproximación no vulneren el funcionamiento del mecanismo, estructura, prototipo... que se ha aplicado.

Toda investigación comienza por la observación metódica y sistemática de los fenómenos y hechos que suceden en el mundo que nos rodea. Como resultado de esa observación, se generan diversos interrogantes y dudas que llevan al planteamiento de un problema.

Una vez definido dicho problema, el observador, con toda la información disponible, da una respuesta probable al cuestionamiento planteado: formula hipótesis. Como ésta es una suposición, debe ser corroborada por medio de la experimentación, para determinar su validez.

De acuerdo con la hipótesis formulada, es posible prever consecuencias que habrán de presentarse en los hechos o fenómenos que se investigan, es decir, establecer predicciones.

Luego se debe comprobar si dichas predicciones son correctas, para lo cual se realiza la experimentación.

Las hipótesis científicas son fructíferas en la medida que permiten establecer predicciones, y el experimento constituye la prueba de la validez de las predicciones efectuadas.

El trabajo experimental proporciona resultados e información que el investigador somete al análisis y a la interpretación.

De ese modo, se llega a elaborar las conclusiones correspondientes a la investigación realizada.

Entonces, los datos obtenidos experimentalmente constituyen el núcleo fundamental del trabajo de investigación y su correcto análisis e interpretación resulta un aspecto importantísimo para elaborar conclusiones confiables.

En caso de que la conclusión no demuestre la corrección de la hipótesis formulada, es necesario formular nuevas hipótesis y reanudar las acciones tendientes a comprobar su validez.

Cuando la conclusión confirma la hipótesis y puede ser aplicada a todos los fenómenos semejantes, se esta en presencia de una generalización, la cual a su vez, puede derivar de la formulación de una ley o principio, con los cuáles se elaboran teorías.

Las conclusiones constituyen conocimientos o informaciones básicas que deben motivar para realizar nuevas investigaciones por los interrogantes que dejan planteados.

Leyes. Constantes físicas

De los principios y de sus aplicaciones a fenómenos determinados y concretos se extrae la Ley Física. Ésta es pues, en general, un hecho, una verdad restringida por la aplicación de los principios a circunstancias particulares de instrumentación y medio; concreta la medida de las magnitudes físicas permitiendo, en fin, establecer relaciones de variación entre unas y otras. Expresada la ley mediante una fórmula matemática significa una idea, debiendo ser por su reducido alcance lo más sencilla posible.  Podríamos afirmar que una ley Física tiene una configuración conceptual y significación sencilla y clara. En su forma más general podríamos expresar matemáticamente una ley de la siguiente forma: a = f (b, c, d,...). Es decir, el valor de la magnitud a depende de los valores de las magnitudes b, c, d, etc.

Las Constantes Físicas que intervienen en las fórmulas que expresan las leyes, pueden ser Universales o Circunstanciales, según que su valor sea siempre el mismo, cualesquiera que sean las condiciones del lugar, tiempo, temperatura, etc., o bien dependa de las condiciones en que el fenómeno se realiza. Ejemplos: la constante de gravitación G, la de los gases perfectos R, la carga de un electrón e son constantes universales. La velocidad inicial v₀, la constante de la ley de Boyle-Mariotte K, el coeficiente dieléctrico de un medio e... son constantes circunstanciales.

Teoría y teorema

Un paso más adelante en el desarrollo estructural de la elaboración sistemática nos lleva a considerar el término genérico de Teoría, entendiéndose como tal la deducción y planificación de los fenómenos particulares que, a la luz de principios y leyes, pueden ser estudiados y comprendidos.

Como instrumento inseparable del desarrollo teórico acudimos en general a la lógica y en particular al razonamiento matemático.

Llegamos finalmente a la cúspide de esta gran pirámide científica que constituye la Física mediante la aceptación de las conclusiones lógico-matemáticas que la formulación de una Ley nos determina y que denominamos con la palabra Teorema. Expresión sencilla del símbolo matemático a que reducimos el fenómeno científico, que sintetiza la esencia del fenómeno mismo. 

 

MAGNITUDES FÍSICAS. UNIDADES

Magnitud y Cantidad

Magnitud es todo aquello susceptible de medida. Ejemplo: La longitud, la masa, el tiempo, son magnitudes, ya que pueden medirse. Medir es comparar dos magnitudes de la misma especie, una de las cuales se toma como Unidad.

Ejemplo: Si A y B son magnitudes de la misma especie, y se toma A como unidad, el número de unidades A que se necesitan para hacer una magnitud igual a B expresa la medida de B.

Cantidad de una Magnitud es el número de unidades a que es equivalente dicha magnitud. Ejemplo: El tiempo es una magnitud; siete años es una cantidad.

Unidad: expresión de una medida

Unidad es una cantidad arbitraria que se adopta para comparar con ella cantidades de su misma especie. En la elección de una unidad influye la extensión de la cantidad a medir. Ejemplos:

Para la medida de la distancia de la Tierra a una estrella de las llamadas lejanas escogeremos el año luz; para la distancia entre dos ciudades el kilómetro; en la venta de un cable el metro; en la medida del espesor de una lámina el milímetro y para la medida de la longitud de onda de la luz el angstrom (Å). No es necesario que sean éstas las unidades empleadas; siempre que nos convenga podemos tomar como unidad cualquier cantidad arbitraria: si llamamos A a una cantidad (superficie en la Fig. I-1), la cantidad B equivale a 4A; hemos medido B adoptando A como unidad.

La expresión de una medida es un número concreto, es decir, un número (veces que la cantidad contiene a la unidad) seguido del nombre o expresión de la unidad empleada en la medida (500 kilómetros; 26 metros; 2 milímetros).

Condiciones que debe reunir la unidad. Unidad natural

En toda unidad de medida se debe poder determinar la igualdad y la suma. Ejemplo: adoptada una determinada longitud como unidad metro, ha de poder establecerse qué magnitud es igual a un metro y qué magnitud contiene dos, tres, cuatro veces a nuestra unidad. De aquí nace el concepto de múltiplo (1km = 1 000 m) empleado, a su vez, como unidad en medidas adecuadas.

Este criterio de suma, que nos lleva a establecer múltiplos, nos da como consecuencia la posibilidad de conseguir submúltiplos o divisores de la unidad, pues si el km se puede dividir en 1 000 partes iguales (metro), el metro tiene necesariamente de la misma propiedad, obteniéndose fracciones de la unidad que, a su vez, nos sirven como unidad cuando pueda interesarnos.

Con la intención de llegar a establecer unidades únicas adoptadas universalmente para lo que llamaremos magnitudes fundamentales, y siempre con la idea de elegir conveniente el término adecuado para la extensión de la cantidad a medir, los organismos de carácter internacional [La Conferencia General de Pesas y Medidas (CGPM), el Comité Internacional de Pesas y Medidas (CIPM) y la Unión Internacional de Física Pura y Aplicada (UIFPA)] recomiendan para prefijos, símbolos y valores correspondientes a las unidades simples del Sistema Internacional (SI), que posteriormente definiremos, los indicados en la tabla adjunta.

Un proceder unánime en esta línea, nos proporcionaría un mejor entendimiento y una mayor fluidez en el lenguaje científico, además de una mejor comprensión en el orden de la magnitud de la cantidad a medir. Ejemplo: debemos tener en cuenta que para expresar una fuerza determinada, 1 kilogramo-fuerza por ejemplo, también se puede decir 10 newton o 10⁶ dinas; o que 1 caballo de vapor es 75 kilográmetros por segundo o 735 joule por segundo; esta pluralidad de formas para expresar lo mismo, es indudable que desconcierta al estudiante y le dificulta el “darse cuenta” de la cantidad expresada.

Existen en la naturaleza cantidades de una magnitud sin posibilidad de poderse encontrar divisores de ella, a tal cantidad la llamamos Unidad Natural de la magnitud; existen múltiplos enteros de ella pero nunca una fracción. Decimos de tal magnitud que está “cuantificada” y a la unidad la llamamos “quantum”. Así por ejemplo: la energía luminosa que emite un foco no varía de forma continua, existe para cada frecuencia una cantidad mínima, llamada “fotón” y que es indivisible.

La unidad natural de energía electromagnética es la energía de un fotón.

Magnitudes fundamentales y suplementarias

Son magnitudes fundamentales aquellas cuyas unidades se eligen arbitrariamente tomándose como base de los sistemas de unidades y no tienen una ecuación que las defina.

Como los fenómenos físicos se realizan en el espacio mientras transcurre el tiempo; la Naturaleza nos impone, así, dos magnitudes fundamentales: Longitud (L) y Tiempo (T), sin definición precisa, cuya existencia conocemos desde que se inicia nuestra razón.

En la parte de la Física llamada Mecánica, es necesaria una tercera magnitud fundamental definida por nuestra propia intuición que, con las dos anteriores, permita definir de una manera coherente las demás magnitudes que intervienen en los fenómenos mecánicos; tal magnitud se elige arbitrariamente: en Física teórica se usa la Masa (M) y en la técnica la Fuerza (F).

Muchos fenómenos físicos varían según la homogeneidad del espacio, en particular en electricidad, teniendo que introducir para su estudio, otra magnitud fundamental llamada Coeficiente Dieléctrico o Permitividad (e) que nos mide la variabilidad del espacio, desde el vacío hasta el más complicado medio heterogéneo; o bien, ésta quedará definida si se toma a la Intensidad de Corriente (A) como magnitud fundamental, por lo que puede tomarse como tal a la una o a la otra.

Al variar el “equilibrio energético” dentro del “caos molecular” en los sistemas físicos, es necesario para el estudio de la Termología introducir como magnitud fundamental. No pudiendo ser eludido, que los fenómenos ópticos, deban ser observados por nuestros ojos, y que la retina tenga unas propiedades que provocan gran variedad de sensaciones, cuya medida entra dentro de la Psicología Experimental, se hace necesario introducir en el estudio de la Fotometría la magnitud fundamental Intensidad Luminosa (J) que de alguna manera nos mide la sensación de luminosidad en el ojo humano.

Como se verá más adelante, es necesario distinguir entre la magnitud fundamental masa y la que vamos a llamar Cantidad de Sustancia, (N); completándose, con esta última elección arbitraria, el cuadro de magnitudes fundamentales (L, T, M, A, q, J y N) que actualmente se utilizan en Física.

Son Magnitudes Suplementarias, El Ángulo Plano, definido como la porción de plano limitada por dos semirrectas que parten de un mismo punto; a este punto se le llama vértice y a las semirrectas lados del ángulo; y el Ángulo Sólido definido como cada una de las porciones del espacio limitadas por una superficie cónica. Ambas magnitudes son puramente geométricas y todavía no se ha decidido si son fundamentales o derivadas.

Unidades patrones

Elegidas convencionalmente las magnitudes fundamentales (como se explicará más adelante), los diferentes Congresos Científicos Internacionales fijaron las unidades llamadas PATRONES, cuyas definiciones han ido variando con las exigencias de superior precisión en las técnicas metrológicas, y que exponemos a continuación.

·              La unidad de LONGITUD es el METRO (m): distancia a cero grados celsius, entre dos trazos paralelos hechos en una barra de platino con 10% de iridio, que se conserva en el Museo Nacional de Pesas y medidas de Sevres, París, aproximadamente igual a la diezmillonésima parte del cuadrante del meridiano terrestre. El 16 de octubre de 1960 la Conferencia General cambió la definición clásica del metro, tomando como nuevo patrón (nuevo metro) a 1.650.763,73 longitudes de onda, en el vacío, de la radiación correspondiente a la transición entre los niveles 2p⁵ y 5d¹⁰ del átomo de criptón 86. Debido a las constantes exigencias de superior precisión, en octubre de 1986 la Conferencia General de Pesas y Medidas celebrada en esta fecha en París, define nuevamente el metro como la longitud recorrida en el vacío por las ondas electromagnéticas durante un tiempo de 1/299 792 458 de segundo (lo que nos indica que la velocidad de estas ondas es 299 792 458 m/s). (Obsérvese que la tendencia en la búsqueda de un patrón internacional es que su definición sea de naturaleza universal, y no basada en ningún artilugio artificial susceptible de variaciones temporales).

·              La unidad de MASA es el KILOGRAMO (kg), es la masa del prototipo de platino iridiado sancionado por la Conferencia General de Pesas y medidas en 1901 y depositado en el pabellón de Bretenil de Sevres. Este prototipo tiene forma cilíndrica, contiene aproximadamente el 90% de platino y el 10% de iridio, y su masa es muy aproximada a la de un litro de agua destilada a cuatro grados centígrados. Actualmente se define en función de la masa de los átomos como se verá más adelante.

·              La unidad de TIEMPO es el SEGUNDO (s): 1/86 400 del día solar medio. (86 400 es el número de segundos del día solar medio, que se obtiene multiplicando 24 horas del día, por 60 minutos de la hora y por 60 segundos del minuto). DÍA SOLAR MEDIO es la duración media de los días solares del año, determinadas por el tiempo que tarda el Sol, en su movimiento aparente en realizar un giro en torno a la Tierra. La XI conferencia General de Pesas y medidas de 1960 definió el SEGUNDO como la fracción igual a 1/31 556 925,974 7 del año trópico para enero de 1900, cero a doce horas del tiempo efemérides.

Si bien, el patrón segundo astronómico es más exacto que el segundo solar medio, se necesitaba de un patrón material comparable a los prototipos metro patrón y kilogramo patrón; por lo que la XIII Conferencia General de 1967-68, adoptó para EL SEGUNDO el patrón atómico de frecuencia definido como la duración de 9 192 631 770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133.

·              La unidad de INTENSIDAD DE CORRIENTE ELÉCTRICA es el AMPERIO (A) definido como la intensidad de una corriente eléctrica constante que, mantenida entre dos conductores paralelos rectilíneos, de longitud infinita, de sección circular despreciable y colocados en el vacío a una distancia de un metro uno de otro, produce entre estos dos conductores una fuerza igual a 2x10^-7 newton por metro de longitud.

·              La unidad de TEMPERATURA es el KELVIN (K) definido como grado de la escala termodinámica de las temperaturas absolutas, en la cual la temperatura del punto triple del agua es 273,16 K, por tanto “es la fracción 1/273,16 de la temperatura termodinámica del punto triple del agua”.

·              La unidad óptica de INTENSIDAD LUMINOSA es la CANDELA (cd) definida como “la intensidad luminosa en una dirección determinada de una abertura perpendicular a esta dirección, que tenga una superficie de 1/600 000 metro cuadrado y radie como una radiador integral o cuerpo negro a la temperatura de fusión del platino (2 043 K = 1 770 ºC), bajo la presión de 101 325 pascales”.

Sistemas de unidades

Llamamos SISTEMA DE UNIDADES al conjunto de éstas que resulta de escoger determinadas unidades simples. La elección del sistema de unidades no se hace, en general, atendiendo a las magnitudes fundamentales; puesto que se eligen unidades simples que tienen con las fundamentales una dependencia funcional. Así, por ejemplo, elegimos en el sistema técnico como unidad por su dependencia con la masa, la magnitud fuerza. Esta unidad es el kilopondio o KILOGRAMO-FUERZA; fuerza con que el kilogramo patrón es atraído hacia la Tierra, al nivel del mar y 45º de latitud. En este sistema la unidad de masa es una unidad derivada y se llama UNIDAD TÉCNICA DE MASA.

Ya hemos indicado la conveniencia de tomar universalmente un único sistema de unidades; hoy por hoy es una cuestión de adaptación y tránsito por lo que el lenguaje científico no está sujeto a las normas dadas por las CGPM, teniendo el lector que adquirir cierta flexibilidad en el empleo de sistemas de unidades, lo cual le facilitará la comunicación entre personas cuyos intereses particulares están situadas en diversos campos; por lo que entramos a definir los distintos sistemas que hoy suelen utilizarse, pero siempre, dándole la máxima importancia al que llamaremos sistema internacional.

En mecánica emplearemos los siguientes sistemas: SISTEMA CEGESIMAL (CGS); sus unidades simples son el centímetro de longitud, el gramo de masa y el segundo de tiempo. SISTEMA GIORGI (G), o MKS; sus unidades simples son el metro de longitud, el kilogramo de masa y el segundo de tiempo. SISTEMA TÉCNICO; sus unidades simples son: el metro, el kilogramo fuerza y el segundo.

En electricidad emplearemos: SISTEMA DE UNIDADES ELECTROSTÁTICAS; sus unidades simples son el centímetro de longitud, el gramo de masa, el segundo de tiempo y el coeficiente dieléctrico para el vacío e₀ =1/4p  SISTEMA GIORGI ELÉCTRICO; sus unidades simples son el metro de longitud, el kilogramo de masa, el segundo de tiempo y el amperio de intensidad.

SISTEMA INTERNACIONAL (SI): sus unidades simples son el metro de longitud, el kilogramo de masa, el segundo de tiempo, el amperio de intensidad, el kelvin de temperatura, la candela de intensidad luminosa y el mol de cantidad de sustancia. Como vemos es el sistema GIORGI AMPLIADO, cuya extensión debe hacerse a todo tipo de aplicación Científica o Técnica, es el más frecuentemente utilizado.

En este sistema se distingue entre MASA, “como coeficiente característico de cada partícula o cuerpo, que determina su comportamiento cuando interactúa con otras partículas”, y la magnitud CANTIDAD DE SUSTANCIA que nos define “la cantidad de elementos o composiciones químicas que llevan los cuerpos”; esta magnitud es diferente de la masa y evidencia que la antigua definición de masa como cantidad de materia es errónea.

Se define el MOL como: “la cantidad de sustancia de un sistema que contiene tantas entidades elementales (átomos, moléculas, iones...) como átomos de carbono hay en 0.012 kilogramos de Carbono 12». Su símbolo es «mol”; el valor de 1 u (UNIDAD UNIFICADA DE MASA ATÓMICA), será, teniendo en cuenta que 1 u es “la doceava parte de la masa de un átomo del isótopo 12 del Carbono” y que “0,012 kg de Carbono 12 contiene 6,022x10²³ átomos/mol (NÚMERO DE AVOGADRO):

1u =0,012/12x6,022x10²³= 1,6606x10⁻²⁷Kg

Así por ejemplo sabemos que un mol de hidrógeno contiene dos gramos de hidrógeno, uno de oxígeno contiene 32 gramos de oxígeno, uno de agua 18 gramos de agua... Luego iguales cantidades de sustancia (un mol) contienen generalmente diferentes masas; diferencia evidente entre masa y sustancia. En una reacción química pueden variar el número de moles sin cambiar la masa.

También es importante la medición del sistema ABSOLUTO INGLÉS, utilizado en los países de habla inglesa, en los que se eligen como unidades simples: el pie de longitud, la libra de masa, el segundo de tiempo, y el amperio de intensidad de corriente.

Presentamos a continuación, algunas unidades distintas a las ya definidas, que son normalmente utilizadas en los distintos medios de trabajo; dando su equivalencia en el SI:

 

Magnitudes derivadas. Medidas indirectas

Una Magnitud es Derivada cuando se define empleando magnitudes simples. Ejemplo: al decir que un automóvil lleva una velocidad de 60 kilómetros por hora, nombramos una cantidad que corresponde a una magnitud derivada o compuesta, ya que en su determinación necesitamos la medida de una longitud (por medio de carteles que nos señalan distancias en la carretera, por ejemplo) y de un tiempo (por medio de un reloj o un cronómetro), la velocidad es una magnitud derivada.

Las magnitudes fundamentales o simples, son elegidas convencionalmente, las demás tendrán que depender de ellas; por tanto, el que una magnitud sea simple o derivada será arbitrario. Ya hemos indicado que en el CGS y SI la masa es fundamental, y derivada en el sistema TÉCNICO.

Realizamos una medida indirecta cuando medimos una cantidad en función de otras que se relacionan con aquella por medio de una fórmula matemática.

La determinación de una magnitud derivada requiere:

 a) Su definición correcta, clara y concisa.

 b) Establecer una fórmula matemática en la que se compendien todas las ideas expresadas en la definición.

 c) Fijar unidades de medida.

Una vez comprendida y aprendida la definición de una magnitud física, hay que expresarla por medio de una fórmula. La Fórmula, en Física, la expresión de una idea. Por ejemplo, cuando se define velocidad media como “el desplazamiento recorrido en la unidad de tiempo” y si llamamos Δx al desplazamiento o camino recorrido y Δt al intervalo de tiempo empleado en recorrerlo, formularemos sin duda:

Velocidad media = Desplazamiento/Intervalo de tiempo = Δx/Δt

Unidades derivadas y suplementarias

Para fijar unidades derivadas, basta considerar la fórmula de la magnitud, expresando las unidades simples en el sistema que se desee adoptar.

De acuerdo con las XII y XIV Conferencia General de Pesas y Medidas, adoptamos como unidades suplementarias y derivadas las que se definen en el siguiente cuadro:

La unidad de magnitud suplementaria Ángulo Plano es el Radián (rad) definido como: ángulo plano que, teniendo su vértice en el centro de un círculo, intercepta sobre la circunferencia de este círculo, un arco de longitud igual al radio.

El Sistema Métrico Legal Argentino (SIMELA)

Durante muchos años existió una verdadera anarquía en las unidades usadas para las diferentes magnitudes. Cada país o región tenía las suyas y a veces existían diferencias dentro de un mismo país. Así, por ejemplo, en el caso de la longitud, se fue evolucionando desde formas poco precisas, como el palmo, el paso, el codo, hasta llegar al metro, utilizado en la actualidad, y pasando por otras unidades, tales como el pie, la pulgada, la vara y otras que aun se siguen utilizando en algunos países y lugares, así como también en algunas actividades que se desarrollan en nuestro país (por ejemplo, en la medición de maderas).

Finalmente, tras un largo proceso de homogeneización que ha abarcado muchos siglos se llegó a establecer, en 1960 por la CGPM el denominado SI. Éste fue adoptado por nuestro país en 1972 por Ley Nacional N° 19511 con la denominación de Sistema Métrico Legal Argentino.

Este sistema esta elaborado sobre la base del Sistema Internacional de Unidades (SI) con el agregado de unas pocas unidades no pertenecientes al SI pero admitidas, tales como: el litro, la hora, el minuto, etc. El SIMELA consta de unidades de base, unidades suplementarias y unidades derivadas.

Unidades de base.

Unidades agregadas.

Las unidades más importantes agregadas al SI por Ley Nacional 19511 son:

Para la escritura de los nombres y símbolos de las unidades se han establecido normas concretas, tales como:

·   Los símbolos deben escribirse con letras romanas rectas y nunca deben pluralizarse. Ej: kg y no kgs; m y no mts; h y no hs.

·   No deben colocarse los símbolos con punto final salvo cuando finaliza la oración. Ej: kg y no kg.; m y no m.; h y no h.; etc.

·   Los símbolos de las unidades se deben escribir con letras minúsculas, excepto cuando el nombre de la unidad deriva de un nombre propio. Ej: m; kg; A; J.

·   Aunque la unidad de volumen es el metro cúbico, se admite el uso del litro, pudiendo utilizarse como símbolo la “ele” minúscula o mayúscula, según se prefiera.

·   En temperatura puede usarse la unidad derivada del grado Celsius, aclarando que no es centígrado y que su símbolo es °C. Ej: 37 °C y no 37° C (los símbolos ° y C son inseparables).

·   Cuándo se escribe el nombre de la unidad siempre debe hacerse con minúscula. Ej: metro; segundo; pascal.

·   No se deben castellanizar los nombres de las unidades. Ej: joule y no julio; volt y no voltio.

·   Cuando se multiplican dos unidades se coloca un punto entre ellas. Ej: N.m; N.s .

·   En el caso de una multiplicación conviene eliminar la palabra “por”. Ej: newton segundo y no newton por segundo. En cambio, cuando se trata de un cociente sí se utiliza la palabra “por”. Ej: m/s= metro por segundo; kg/m³ = kilogramo por metro cúbico.

·   Cuándo se trata de una unidad formada a partir de otros dos pos división, puede utilizarse una barra, una línea horizontal o potencia negativa. Ej: m/s ó m.s^-1.

Múltiplos y submúltiplos de la unidades

Cuando el valor de una cantidad es un número muy grande, o por el contrario, muy pequeño, se suelen emplear los múltiplos y submúltiplos de la unidad.

Por ejemplo: Unidad de longitud: el metro

Si observamos con atención vemos que los nombres de cada múltiplo y submúltiplo se forman colocándole un determinado prefijo a la unidad metro. Precisamente, el Sistema Internacional de unidades, establece cuáles son los prefijos que pueden usarse para las distintas unidades:

También se indica que se debe aplicar un solo prefijo por cada unidad. Ej: 0,000 000 001 es igual a 1 nm (nanómetro) y no 1mμm (milimicrómetro)

Análisis Dimensional. Toda magnitud derivada se puede expresar por medio de un producto, ECUACIÓN DE DIMENSIONES, de las unidades simples y expresan la manera de intervenir en su formación.

Consistencia y conversiones de unidades

Usamos ecuaciones para expresar las relaciones entre cantidades físicas representadas por símbolos algebraicos. Cada símbolo denota siempre un número y una unidad. Por ejemplo, d podría representar una distancia de 10 m, t un tiempo de 5 s y v una rapidez de 2 m/s.

Toda ecuación debe ser dimensionalmente consistente. No podemos sumar manzanas y automóviles; s´lo podemos sumar o igualar dos términos si tienen las mismas unidades. Por ejemplo, si un cuerpo que viaja con rapidez constante v recorre una distancia d en un tiempo t, estas cantidades están relacionadas por la ecuación

d =v.t

si d se mide en metros, el producto v t también debe expresarse en metros. Con los números anteriores, escribimos:

10 m = 2(m/s) 5 s

Como la unidad 1/s del miembro derecho de la ecuación cancela a s, el producto v. t esta en metros, como debe ser. En los cálculos, las unidades se tratan igual que los símbolos algebraicos en cuanto a la multiplicación y la división.

Perímetros, Áreas y volúmenes de cuerpos geométricos regulares.

Magnitudes Vectoriales:

¿Cuáles son los elementos de un vector?

–        Intensidad o modulo: es la medida del vector, se indica mediante un número y una unidad.

–        Dirección: se considera la recta de acción que contiene al vector. Ejemplo vertical, horizontal u oblicuo.

–        Sentido: una recta tiene dos sentidos y se identifica a la correcta por flecha. Ejemplo: una flecha que apunte a la  derecha, izquierda, arriba, abajo, etc..

“La fuerza es una magnitud vectorial porque para especificarla completamente deben indicarse, su intensidad, su dirección y su sentido.”

 “Para representar varias fuerzas de un sistema habrá que adoptar una escala de fuerzas, para lo cual debe establecerse una escala única de manera tal que todas las fuerzas que constituyan el sistema pueden ser representadas convenientemente: La mayor fuerza debe estar contenida en la hoja y la menor debe ser aceptablemente visible

Ejemplo: Establecer una escala para representar una fuerza de 150N. La N es la unidad de medida y se llama Newton. Si tenemos una fuerza de F = 150 N hacia la derecha nuestra escala de fuerza podría ser:

                                                      Esc = 30 N                                                          

                                                                 cm                         

Esc. es llamada escala de fuerza e indica cuantos néwtons son representados por un centímetro.

Si queremos saber que longitud del vector que representará una fuerza de 150 N, bastará dividir el valor de la fuerza por el de la escala. De esta manera 150 N dividido en 30 N/cm nos da 5 cm. La representación gráfica es la siguiente:

Si en otro caso queremos saber el valor de la fuerza se deberá multiplicar el valor de la escala por la longitud del vector.

§  El conjunto de fuerzas que actúan sobre un cuerpo se denomina sistema de fuerzas.

Ejemplo: Cuando varias fuerzas actúan en un cuerpo en reposo, este inicia un movimiento en una sola dirección aunque las fuerzas se ejerzan sobre el en distintas direcciones. Esto es porque el efecto de todas las fuerzas sumadas es único.

Hay diferentes formas de sumar fuerzas dependiendo de sus direcciones. La clasificación que se puede hacer es la siguiente:

Colineales: cuando todas las fuerzas del sistema tienen la misma recta de acción

Concurrentes: las fuerzas actuantes tienen la propiedad de concurrir a  un único punto.

Paralelas: las fuerzas actuantes tienen rectas de acción paralelas.

Perpendiculares: cuando dos fuerzas entre si forman un ángulo de 90º.

Composición de las fuerzas

Hallar la resultante R de un sistema de fuerzas equivale a componer fuerzas, es decir, a hallar una única fuerza que ejerza el mismo efecto físico de todas.

Encontrar la resultante de un sistema de fuerzas colineales es sencillo, pues en este caso se puede operar directamente con la intensidad de esas fuerzas, representada por el módulo de los vectores, sumándolas si las fuerzas tienen igual sentido, y restándolas si tienen sentidos opuestos. En este último caso la resultante tendrá el mismo sentido que la fuerza de mayor intensidad.

Cuando dos fuerzas de distinto sentido tienen la misma intensidad resul ltante de un sistema de fuerzs colinealess, la resultante R de un sistema es la sujma vectorialntementes de su intensidad, la resultante es el vector nulo y se dice entonces que el sistema está en equilibrio.

Finalmente Uds. van a pensar un ejemplo para cada caso  y vamos a considerar su resolución en forma gráfica y analítica, es decir, características del vector resultante: dirección, intensidad y sentido.

 

 

Para calcular la resultante de fuerzas paralelas, la intensidad y sentido se calcula de la misma manera que el anterior, pero para el punto de apoyo se utiliza un método grafico diferente:

De manera analítica las distancias y la resultante R se calculan:

R=F₁+F₂

R/AB = F₁/B0 = F₂/A0

Para fuerzas concurrentes o perpendiculares se utiliza un método grafico diferente: 

Como se ve en cada grafica los vectores A y B no cambian de dirección, cambian de ubicación pero no de dirección y sentido, menos de cantidad. Apreciando el cálculo grafico de R₁ vemos que la cola del vector A se une a la punta del vector B, y esta resultante se obtiene uniendo en línea recta la cola del vector B a la punta del vector A, y la punta del vector R₁coinside con la punta del vector A, este método grafico se representa A+B. De la misma manera se obtiene R₂, solo que esta vez unimos la cola del vector B a la punta del vector A, y la resultante R₂ se obtiene uniendo en línea recta la cola del vector A a la punta del vector B, y se representa B+A. Como se puede apreciar R₁ y R₂ son iguales, ya que tienen el mismo modulo, dirección y sentido, es decir que la suma de dos vectores tiene propiedad conmutativa (A+B = B+A).

Para obtener R₃, que es resta entre vectores, se une ambos vectores cola con cola, y luego se traza una línea recta entre las puntas de los vectores, A y B, cuya punta del vector R₃ coincide con la punta del vector que es restado, en este caso A, lo cual R₃ se representa como A-B. En el caso de R₄ se hace exactamente los mismo que el anterior, solo que la punta del vector resultante coincide con el del vector B, ya que este es restado ahora, su representación en este caso es ahora B-A. Como se puede ver R₃ y R₄ tienen el mismo modulo y dirección pero distinto sentido, lo cual A-B ≠ B-A, entonces se puede decir que la resta entre dos vectores no es conmutativo.

El método analítico que se utiliza para calcular la resultante es utilizando el teorema del coseno, el cual consiste en conocer el ángulo de separación entre ambos vectores, cuando están unidos cola con cola.

 

Téngase en cuenta que cuando q es igual a 90º, cos q = 0, por lo tanto el teorema del coseno se convierte en el teorema de Pitágoras:

Momento de una Fuerza:

En mecánica newtoniana, se denomina momento de una fuerza (respecto a un punto dado) a una magnitud (pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza con respecto al punto al cual se toma el momento por la fuerza, en ese orden. También se le denomina momento dinámico o sencillamente momento.

Ocasionalmente recibe el nombre de torque a partir del término inglés (torque), derivado a su vez del latín torquere (retorcer). Este término intenta introducirse en la terminología española, bajo las formas de torque o torca, aunque con escasa fortuna, ya que existe la denominación par que es la correcta en español.

El momento de una fuerza  aplicada en un punto P con respecto de un punto O viene dado por el producto vectorial del vector  por el vector fuerza; esto es,

Donde  es el vector que va desde O a P.

Por la propia definición del producto vectorial, el momento  es un vector perpendicular al plano determinado por los vectores  y .

Dado que las fuerzas tienen carácter de vectores deslizantes, el momento de una fuerza es independiente de su punto de aplicación sobre su recta de acción o directriz.

El momento dinámico se expresa en unidades de fuerza por unidades de distancia. En el Sistema Internacional de Unidades la unidad se denomina newton metro o newton-metro, indistintamente. Su símbolo debe escribirse como N m o N•m (nunca mN, que indicaría milinewton).

Si bien es dimensionalmente N·m parece equivaler al julio, no se utiliza esta unidad para medir momentos, ya que el julio conceptualmente es unidad de trabajo o energía, que son conceptualmente diferentes a un momento de fuerza. El momento de fuerza es una magnitud vectorial, mientras que la energía es una magnitud escalar.

No obstante, la equivalencia dimensional de ambas magnitudes no es una mera coincidencia. Un momento de 1 N•m aplicado a lo largo de una revolución completa ( radianes) realiza un trabajo igual a julios, ya que , donde es el trabajo, es el momento y es el ángulo girado (en radianes). Es esta relación la que podría motivar el nombre de “julios por radián” para la unidad de momento, aunque no es correcto.

Cálculo de momentos en el plano

Cuando se consideran problemas mecánicos bidimensionales, en los que todas las fuerzas y demás magnitudes vectoriales son coplanarias, el cálculo de momentos se simplifica notablemente. Eso se debe a que los momentos serían perpendiculares al plano de coplanariedad y, por tanto, sumar momentos se reduciría a sumar tan sólo sus componentes perpendiculares al plano, que son magnitudes escalares.

Si se considera una fuerza aplicada en un punto P del plano de trabajo y otro punto O sobre el mismo plano, el módulo del momento en O viene dado por:

Siendo el módulo de la fuerza, el brazo de momento, es decir, la distancia a la que se encuentra el punto O (en el que tomamos momento) de la recta de aplicación de la fuerza, y el suplementario del ángulo que forman los dos vectores. El sentido de se determina de acuerdo con la regla de la mano derecha.

Ejemplo

Supongamos que tenemos tres llaves que actúan sobre tres tornillos en la forma indicada por las figuras. Se aplica una fuerza F en el extremo de la llave. Es fácil contestar a las siguientes preguntas:

• ¿En qué situaciones se introduce el tornillo?
• ¿En que situaciones se saca el tornillo?
• ¿Cuáles producen el mismo resultado o son equivalentes?.
• Un momento se considera positivo si el tornillo sale, avanza hacia el lector, la llave gira en sentido contrario a las agujas del reloj.
• Un momento se considera negativo si el tornillo entra, la llave gira en el sentido de las agujas del reloj.

Equilibrio de una barra

Supongamos una barra de masa despreciable, que está sujeta por su extremo O.

Si colocamos un peso P a una distancia x del origen. El momento de esta fuerza respecto del origen O es +P·x.

Atamos una cuerda a una distancia y del origen, y tiramos de ella haciendo un ángulo θ con la vertical, tal como se muestra en la figura. El momento de la fuerza F respecto del origen es -F·y·cosθ.

MAQUINAS SIMPLES

Palancas:

Son mecanismos que se usan para transmitir fuerzas, cuyas direcciones y magnitudes pueden pero nunca aumentaran el trabajo producido.

• Son usadas para vencer ciertas fuerzas resistentes, llamadas resistencias (R), mediantes otras llamadas potencias (P).
• En estas máquinas intervienen la ventaja mecánica (V_M).

V_m= R/P

• Es una barra rigida que puede girar alrededor de un punto fijo (apoyo).
• Las distancias entre los puntos de apoyo y la potencia (brazo de potencia) y entre el punto de apoyo y la resistencia (brazo de resistencia)

Tipos de máquinas simples:

• Esto depende de la posición del punto de apoyo respecto a la fuerza resistente R y a la aplicada P.
• Todas las fuerzas que tienden a mover la palanca en sentido horario se las considera negativas, mientras las fuerzas que tienden a mover la palanca en sentido antihorario son positivas.
• Primer género: el punto de apoyo esta entre la potencia y la resistencia.
• Segundo género: la resistencia esta entre el punto de apoyo y la potencia.
• Tercer genero: la potencia esta entre el punto de apoyo y la resistencia.

 

FÍSICA MECÁNICA* Cinemática
* Estática
* Dinámica



Movimiento: se define como el cambio de posición a través del tiempo, es decir si no hay cambio de posición no hay movimiento.


 


Posición: es un punto que representa la ubicación de un cuerpo o móvil en el espacio en un instante de tiempo.


 


Espacio: esta es una dimensión que se clasifican en tres maneras, las rectas (unidimensionales), los planos (bidimensionales), y los volúmenes (tridimensionales).


 


Trayectoria: son las posiciones sucesivas de un cuerpo moviéndose, es decir el camino recorrido por un móvil. Según la forma de la trayectoria el movimiento recibe su nombre.



Desplazamiento: es la unión en línea recta de dos posiciones en una trayectoria, estas posiciones pueden ser llamadas posición inicial y posición final. Esta línea recta es una flecha o vector, el cual la punta de la flecha se la coloca en la posición final.
 

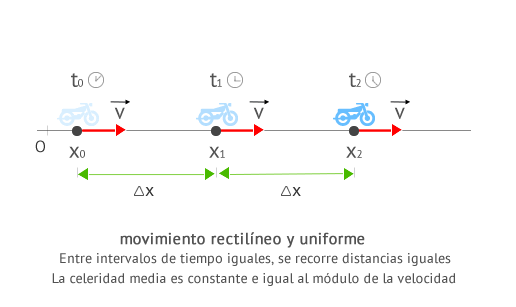
Movimiento rectilíneo

Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.

Posición

La posición x del móvil se puede relacionar con el tiempo t mediante una función x=f(t).
Desplazamiento
Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Dx=x'-x en el intervalo de tiempo Dt=t'-t, medido desde el instante t al instante t'.

Velocidad: es la rapidez o lentitud del cambio de posición dependiendo del tiempo.

Para determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Dt tan pequeño como sea posible, en el límite cuando Dt tiende a cero. Pero dicho límite, es la definición de derivada de x con respecto del tiempo t 

Aceleración: es la rapidez o lentitud del cambio de velocidad dependiendo del tiempo

En general, la velocidad de un cuerpo es una función del tiempo. Supongamos que en un instante t la velocidad del móvil es v, y en el instante t' la velocidad del móvil es v'. Se denomina aceleración media entre los instantes t y t' al cociente entre el cambio de velocidad Dv=v'-v y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio, Dt=t'-t.
La aceleración en el instante t es el límite de la aceleración media cuando el intervalo Dt tiende a cero, que es la definición de la derivada de v.

Movimiento rectilíneo uniforme


 
Movimiento Rectilíneo Uniformemente Variado
 

Movimiento Circular
En cinemática, el movimiento circular es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si, además, la velocidad de giro es constante, se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio fijo y velocidad angular constante.

En los movimientos circulares hay que tener en cuenta algunos conceptos específicos para este tipo de movimiento:
• Eje de giro: es la línea alrededor de la cual se realiza la rotación, este eje puede permanecer fijo o variar con el tiempo, pero para cada instante de tiempo, es el eje de la rotación.
• Arco o ángulo de giro: partiendo de un eje de giro, es el ángulo o arco de radio unitario con el que se mide el desplazamiento angular. Su unidad es el radián.
• Longitud de arco: es la medida del espacio recorrido, longitud de la trayectoria, que realiza el móvil en el movimiento circular
Velocidad angular: es la variación de desplazamiento angular por unidad de tiempo.
• Aceleración angular: es la variación de la velocidad angular por unidad de tiempo.
VELOCIDAD ANGULAR Y TANGENCIAL
 
 
LEYES DE NEWTON
 
 
DIAGRAMA DE CUERPO LIBRE
 
 
TRABAJO DE UNA FUERZA
 
 
Energía:
En física, energía se define como la capacidad para realizar un trabajo, es decir que un cuerpo o partícula tiene energía si es que es capaz de producir trabajo por sí solo, y según de qué forma  ejerza trabajo se caracteriza la clase de energía. Existen varias clases de energía, como eléctrica, calórica, eólica, solar, etc. Un enunciado clásico de la física afirma que la energía no se crea ni se destruye, sólo se transforma. Esto afirma que la cantidad total de energía en cualquier sistema aislado (sin interacción con ningún otro sistema) permanece invariable con el tiempo, aunque dicha energía si puede transformarse en otra forma de energía. En resumen, la ley de la conservación de la energía afirma que la energía no puede crearse ni destruirse, sólo se puede cambiar de una forma a otra (por ejemplo, cuando la energía eléctrica se transforma en energía calorífica en un calefactor).
En mecánica, se denomina energía mecánica a la suma de las energías cinética y potencial.